Outcome Prediction in Mathematical Models of Immune Response to Infection

Participants

  • Manuel Mai
  • Mark Shattuck

Goal 

Understand the effects of patient-to-patient variability on the prognosis of disease outcomes in ordinary differential equation (ODE) models of immune response to infection.

Techniques 

Numerical solution of large numbers of ODEs, random sampling of ODE parameters, machine learning prediction algorithms for prognosis of outcomes.

Lab(s) 

O'Hern lab in collaboration with the Kirby lab at Colorado State University

Project Overview 

We investigate several systems of ordinary differential equations (ODEs) that model the host immune response to a pathogen load. Advantages of systems of ODEs for investigating the immune response to infection include the ability to collect data on large numbers of ‘virtual patients’, each with a given set of model parameters, and obtain many time points during the course of the infection. We implement patient-to-patient variability v in the ODE models by randomly selecting the model parameters from distributions with coefficients of variation v that are centered on physiological values. We use logistic regression with one-versus-all classification to predict the discrete steady-state outcomes of the system. We find that the prediction algorithm achieves near 100% accuracy for v = 0, and the accuracy decreases with increasing v for all ODE models studied. The fact that multiple steady-state outcomes can be obtained for a given initial condition, i.e. the basins of attraction overlap in the space of initial conditions, limits the prediction accuracy for v > 0. Increasing the elapsed time of the variables used to train and test the classifier, increases the prediction accuracy, while adding explicit external noise to the ODE models decreases the prediction accuracy. Our results quantify the competition between early prognosis and high prediction accuracy that is frequently encountered by clinicians.

 

One of the models (model 1) we employ is a four variable set of ODEs with 23 parameters [1] that simulates a host’s response to an infection. The model describes the dynamical interplay between the variables, P (pathogen), N (neutrophil), D (damage), C (cortisol). This system displays three steady states (health, septic death, and aseptic death) as shown in Fig. 1. 

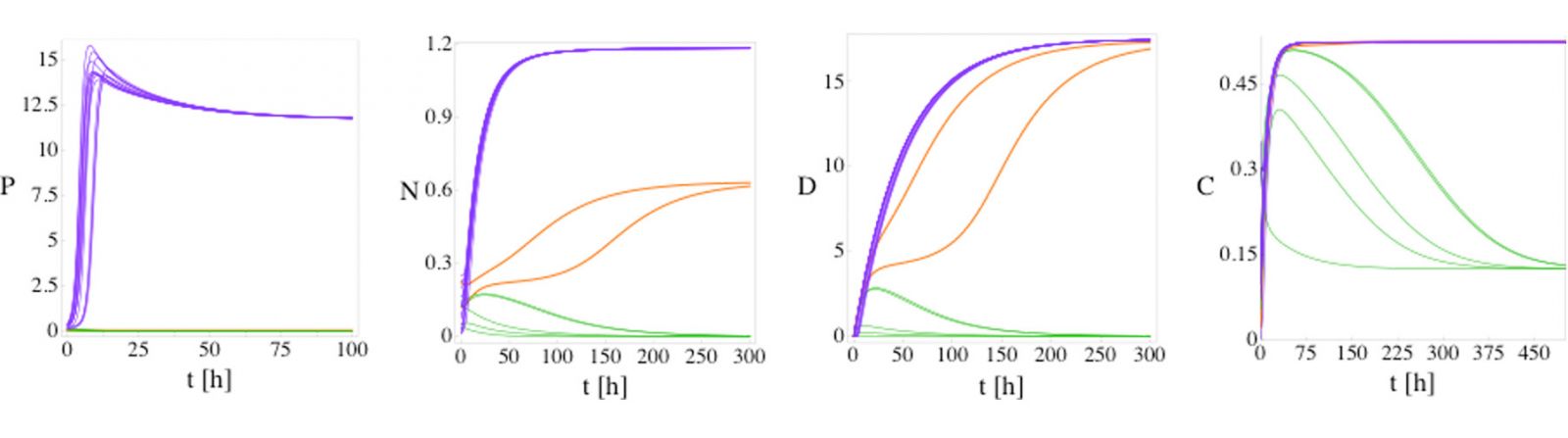
Fig. 1: P, N, D, and C versus time for model (1) from 20 random initial conditions with no patient variation. For a fixed set of parameters model 1 possesses three fixed points: health (green lines), septic death (purple lines), and aseptic death (orange lines). The initial conditions are sampled randomly. The three fixed points can be differentiated by the steady-state values of P and D: health (P = 0, D = 0), aseptic death (P = 0, D > 0), and septic death (P > 0, D > 0). Five, 13, and 2 of the initial conditions evolve to the health, septic death, and aseptic death fixed points, respectively.

To investigate patient-to-patient variability, we sample the patient parameters randomly instead of leaving them fixed. We find that the sets of deterministic ODEs behave stochastically, i.e. the same initial conditions can lead to different disease outcomes.  In this case, the basins of attraction of the fixed points overlap as shown in Fig. 2.

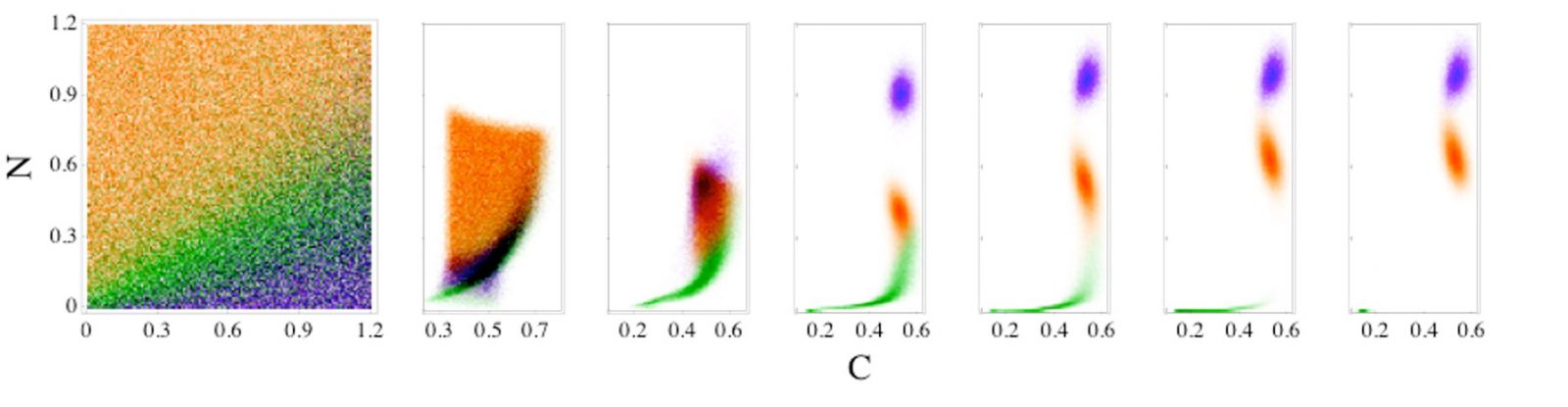
Fig. 2: Time evolution of patient outcomes for a range of neutrophil (N) and cortisol (C) initial conditions for model (1). Patient outcomes in the long-time limit given N and C initial conditions for model [1] are shaded green, orange, and purple for the steady-state outcomes of health, aseptic, and septic death, respectively. The initial values of the pathogen load and damage are fixed, and patient variability is set to 5%. The right six panels indicate how the systems in the leftmost panel separate in the N and C plane as time (in hours) increases, t = 10, 20, 50, 100, 250, and 500, from left to right.

We used a machine learning prediction algorithm to classify different model trajectories into the disease outcomes. The overlap of the basins of attraction poses a fundamental limitation on the prediction accuracy as shown in Fig. 3.

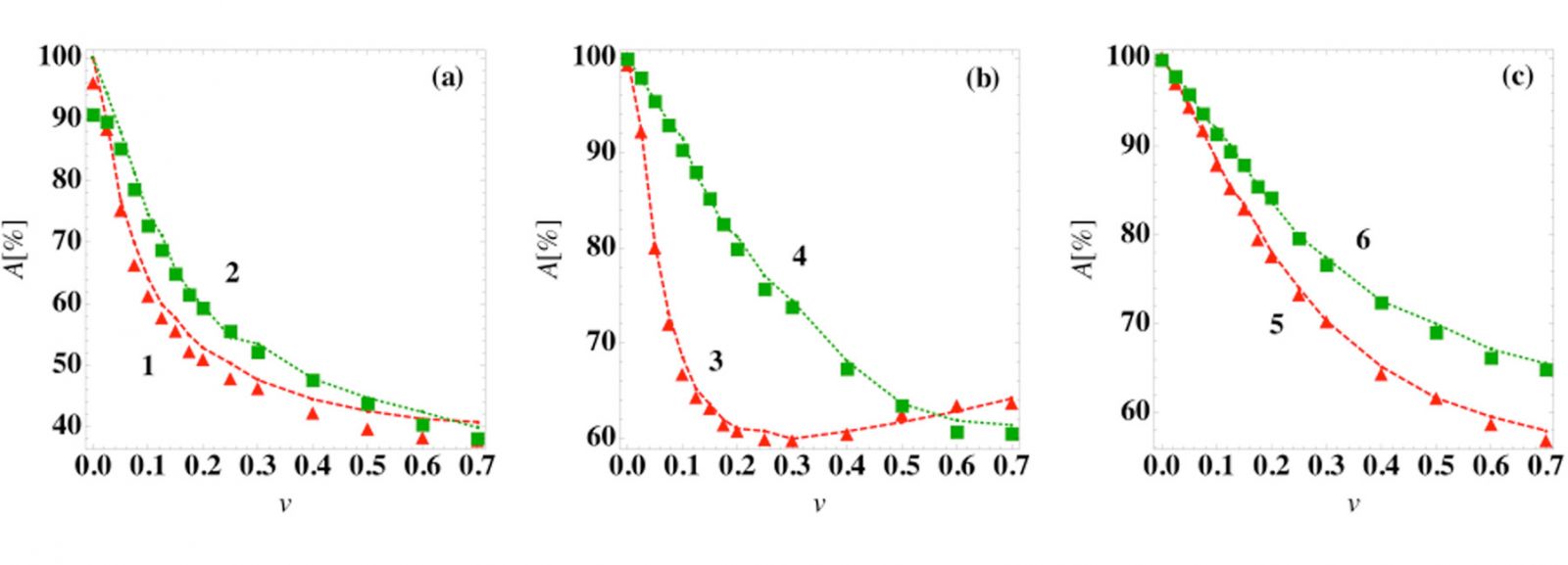
Fig. 3: Prediction accuracy of the steady-state outcome as a function of patient variation. The prediction accuracy A using a logistic regression classifier at time tc = 0 (symbols) and the average best guess over 103 initial conditions (dashed curves) versus patient variation for several ODE models: (a) models (1) and (2), (b) models (3) and (4), and (c) models (5) and (6) in [1].

The basin overlap reduces in time (Fig. 4) because the trajectories move closer to their respective fixed points. This means that the prediction accuracy improves the longer we wait for a prognosis. Late diagnosis, however, means that patients might have to suffer from severe symptoms before we can be sure about the disease outcome. Thus, there is always a tradeoff between early diagnosis and accuracy of the prognosis.

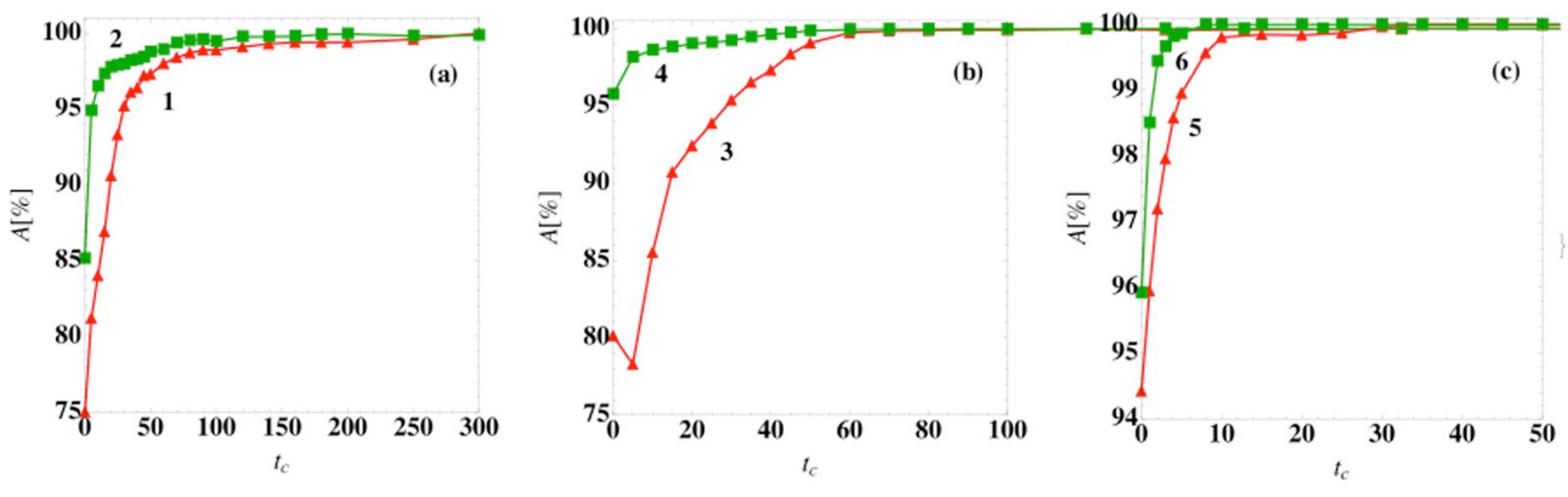
Fig. 4: Prediction accuracy of the steady-state outcome as a function of the classification time. The prediction accuracy A using a logistic regression classifier at time tc (symbols) for (a) models (1) and (2), (b) models (3) and (4), and (c) models (5) and (6) in [1] for patient variation v = 0.05.

 

References:

[1] Mai M, Wang K, Huber G, Kirby M, Shattuck MD, O’Hern CS (2015) Outcome Prediction in Mathematical Models of Immune Response to Infection. PLoS ONE 10(8): e0135861. doi:10.1371/journal.pone.0135861